LeetCode: 行相等的多米诺旋转

题目描述

1007.Minimum Domino Rotations For Equal Row

给定两个数组 tops 和 bottoms，表示一排多米诺骨牌的上下半部分。目标是通过旋转多米诺骨牌，使得 tops 或者 bottoms 中所有的数字相同。目标是最小化所需的旋转次数

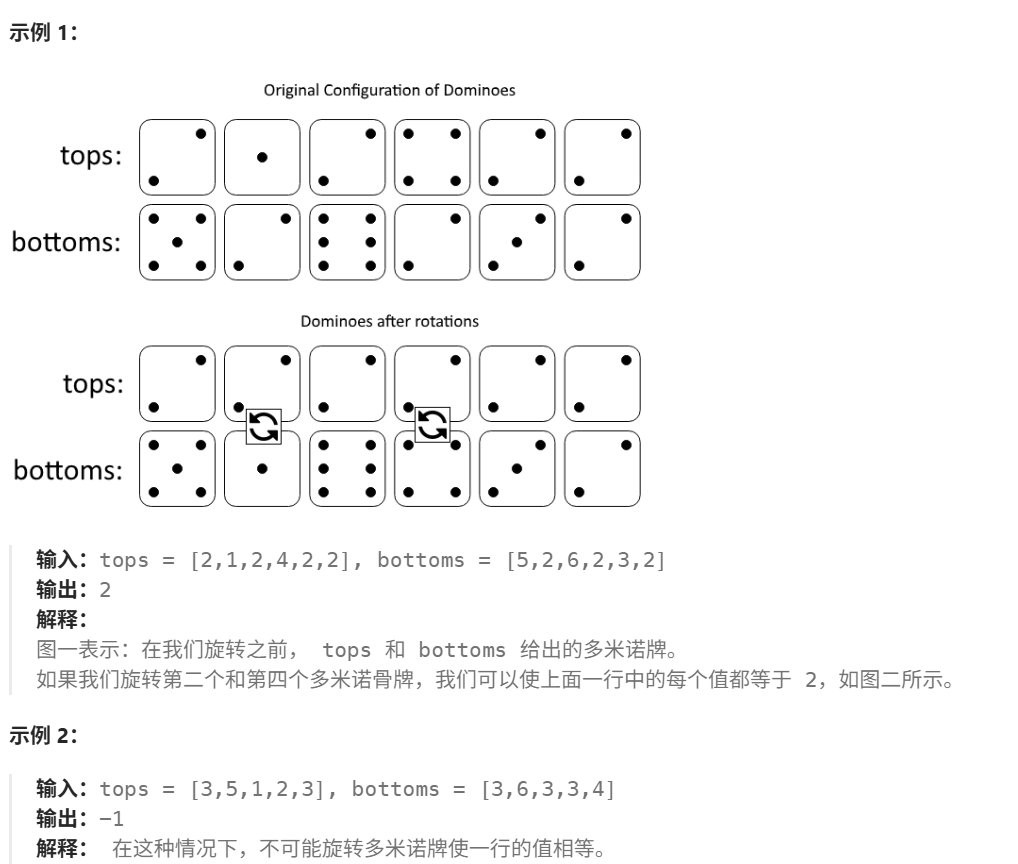
样例

以下是一个输入输出的示例：

Tips:

解题思路

初读题目时，我的第一反应是暴力解法，尝试交换每一个 top[i] 与 bottom[i]，但是这种方法的时间复杂度是，显然无法在限定的时间内通过。

考虑到题目中给定了数字范围，我们可以优化这个过程。我们不必检查所有的数字，而是只需要检查哪些数字可以使得 tops 或 bottoms 在交换后整行都一致。具体来说，我们需要找出数字 num，使得对于每个 i，都满足 tops[i] == num || bottoms[i] == num。

这一步可以通过一次遍历来实现，同时可以将其优化为的时间复杂度。

最初，我考虑使用 集合(set) 来解决问题，但代码实现过于复杂。最终，我选择了 DP 来筛选候选数字。

筛选候选数字

设定 f[i][j] 表示依次检查到bottoms[i] 与 tops[i] 时，数字j 能否使 tops 和 bottoms 数组在交换后变得一致。
对于每个位置，如果 tops[i] 或 bottoms[i] 不等于当前数字，则更新为，表示该数字无法作为目标：

int n = tops.size();
// 创建一个布尔数组 f[7]，用于标记每个数字是否可以作为目标数字
// 数组大小为 7，索引 1 到 6 对应数字 1 到 6，初始时假设每个数字都可行
vector<bool> f(7 , true);

for(int i = 0 ; i < n ; i++) {
    int t = tops[i];
    int b = bottoms[i];

    // 遍历数字 1 到 6，检查这些数字是否可以作为目标数字
    for(int j = 1 ; j <= 6 ; j++) {
        // 如果当前数字 j 与 tops[i] 或 bottoms[i] 相等，则数字 j 仍然是候选数字
        if(j == t || j == b)
            f[j] = f[j] && true;
        // 如果当前数字 j 不能与 tops[i] 或 bottoms[i] 匹配，则标记为不可行
        else
            f[j] = false; 
    }
}

计算最小旋转次数

然后，使用筛选出的数字来计算最小的旋转次数

stack<int> st;
for (int i = 1; i <= 6; i++) {
    if (f[i]) st.push(i); // 选择符合条件的数字
}

if (st.empty()) return -1; // 如果没有任何数字符合条件，返回 -1

int res = INT_MAX;
while (!st.empty()) {
    int target = st.top();
    st.pop();
    int cnt_top = 0, cnt_bottom = 0;
    for (int i = 0; i < n; i++) {
        if (tops[i] == target) cnt_top++;
        if (bottoms[i] == target) cnt_bottom++;
    }
    res = min(res, n - max(cnt_top, cnt_bottom)); // 计算最小旋转次数
}

在这部分代码中，我们从所有可能的候选数字（存储在栈 st 中）中，计算出每个数字变为目标数字所需的最小旋转次数。

完整代码实现

class Solution {
public:
    int minDominoRotations(vector<int>& tops, vector<int>& bottoms) {
        int n = tops.size();
        vector<bool> f(7 , true);

        for(int i = 0 ; i < n ; i++) {
            int t = tops[i];
            int b = bottoms[i];

            for(int j = 1 ; j <= 6 ; j++) {
                // if(j == t || j == b)
                //     f[j] = f[j] && true;
                // else
                //     f[j] = false; 
                  if(j != t && j != b) f[j] = false; // 若数字不能匹配 tops[i] 或 bottoms[i]，则标记为不可行。其余"继承
            }
        }

        int cnt = 0 ;
        stack<int> st;
        for(int i = 1 ; i <= 6 ; i++) {
            if(!f[i]) cnt++;
            else
                st.push(i);
        }
        if(cnt == 6) return -1; // 无交集

        int res = INT_MAX;
        while(!st.empty()) {
            int target = st.top();
            st.pop();
            int cnt_top = 0;
            int cnt_bottom = 0;
            for(int i = 0; i < n; i++) {
                if(tops[i] == target) cnt_top++;
                if(bottoms[i] == target) cnt_bottom++;
            }
            res = min(res, n - max(cnt_top , cnt_bottom));
        }
        return res;
    }
};

总结反思

冗余操作：
- f[j] = f[j] && true 语句是冗余的，可以直接简化为 f[j] = true。
- 使用栈 st 存储候选数字并不必要，直接遍历 f 数组即可。
中间变量不必要：
- 变量 cnt 用来判断无交集的情况并没有实际用处，可以直接在计算过程中处理。
化简为繁
- 其实没有必要筛选必要的数字，因为数字只可能从tops[0] 与 bottoms[0] 中产生。所以要么都变成 tops[0]，要么都变成 bottoms[0]。计算这两种情况，取最小值。

最后附上灵茶山艾府的代码与题解

class Solution {
public:
    int minDominoRotations(vector<int>& tops, vector<int>& bottoms) {
        auto min_rot = [&](int target) -> int {
            int to_top = 0, to_bottom = 0;
            for (int i = 0; i < tops.size(); i++) {
                int x = tops[i], y = bottoms[i];
                if (x != target && y != target) {
                    return INT_MAX;
                }
                if (x != target) {
                    to_top++; // 把 y 旋转到上半
                } else if (y != target) {
                    to_bottom++; // 把 x 旋转到下半
                }
            }
            return min(to_top, to_bottom);
        };

        int ans = min(min_rot(tops[0]), min_rot(bottoms[0]));
        return ans == INT_MAX ? -1 : ans;
    }
};